Draw Circles as Per the Given Number
Radius of a circle is the altitude from the center of the circle to any point on it's circumference. It is ordinarily denoted by 'R' or 'r'. This quantity has importance in almost all circumvolve-related formulas . The area and circumference of a circle are also measured in terms of radius.
Expanse of circle = π (Radius) 2
Definition
A radius is a measure of distance from the centre of any circular object to its outermost edge or boundary. A radius is not only a dimension of a circumvolve simply likewise for a sphere, semi-sphere, a cone with a circular base, a cylinder having circular bases.
A circle tin can be defined as the locus of a signal moving in a plane, in such a fashion that its altitude from a fixed point is always constant. The fixed indicate is known as the centre of the circle and distance between any point on the circle and its heart is chosen the radius of a circumvolve.
Diameter of a Circle
The diameter of a circle is the length of the line starting from i betoken on a circle to some other point and passing through the heart of the circle. Information technology is equal to twice the radius of the circle. It is usually denoted by 'd' or 'D'.
Bore = two x Radius
Or
Radius = Diameter/2
Diameter is the longest chord of the circle.
Besides, nosotros can limited the area and circumference of a circle with respect to the bore.
Circumference of circle = π (Diameter)
Area of circle = π/four (Diameter) 2
Radius, Diameter and Chord
We have already discussed radius and bore of circle. Now suppose, there is a line and a Circumvolve given on a aeroplane. The line could touch circle at ane point, or intersect at 2 points or it could be non-intersecting.
Caption:
Given a line and a Circle, information technology could either be touching the circle, interesting line or not-touching.
Consider any line AB and a circle. And so according to the relative positions of the line and the circle, three possibilities can arise as shown in the given figure.

Line AB intersects the given circle at two singled-out points P and Q. The line AB in this case is referred to as secant of the circumvolve. Points P and Q lie on the circumference of the circle, but they practise not pass through the center of the circle 'O', hence line segment PQ is known every bit a chord of the circle as its endpoints lie on the circumvolve.
Therefore the chord of a circle can be defined as a line segment joining whatever 2 singled-out points on the circle's circumference. A chord passing through the center of a circle is known as the diameter of the circle and it is the largest chord of the circle. This diameter is twice that of the radius of a circle i.east. D=2r, where 'D' is the diameter and 'r' is the radius.
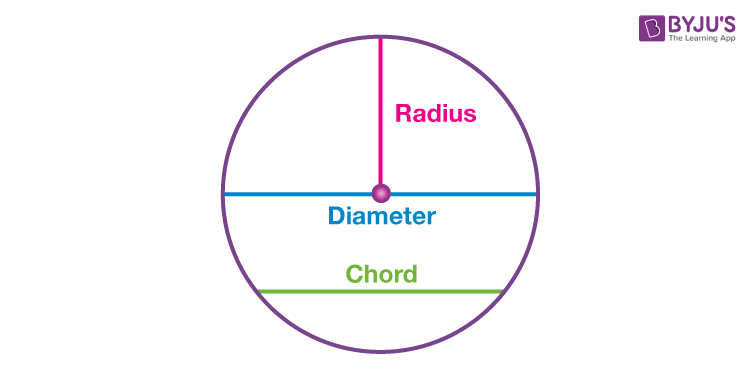
Radius of a circumvolve = Diameter/2
Or
Bore of a circumvolve = 2 ten Radius
Equation
The equation of a circle includes the radius and information technology is given by:
(x-h) 2 + (y-k) two = r 2
Where (h,1000) is the center of circle.
Radius of circle from Area
Since, the formula for area of a circumvolve is given by:
Area of circle = π(Radius) 2
Therefore,
Radius two = Area/π
Radius = √(Area/π)
How to find Radius with Circumference?
If we know the circumference of the circumvolve, and so we can hands find its radius. Let us understand by example.
Suppose, the circumference is 40 cms, then find the radius.
Since, Circumference, C = 2πr
R = C/2π
R = forty/2π
R = 6.37 cm
Radius Formula
With respect to expanse and circumference, we can write the formula for the radius as:
Besides, R = D/ii
Chord of a Circumvolve Theorems
Theorem 1: The perpendicular line drawn from the center of a circumvolve to a chord bisects the chord.

Given: AB= Chord; OC⊥AB
To bear witness: AC=BC
Construction: Draw OA and OB
Proof:
| S. No. | Statement | Reason |
| In ΔOAC and ΔOBC | ||
| 1 | OA = OB | Radii of the same circle |
| two | OC = OC | Mutual |
| three | ∠OCA = ∠OCB | Each angle measure 90 degrees |
| 4 | ΔOAC ≅ ΔOBC | Past RHS congruence criterion |
| 5 | AC = CB | Past CPCT (Corresponding parts of congruent triangles) |
The antipodal of the to a higher place theorem is besides true.
Theorem 2: The line drawn through the center of the circle to bisect a chord is perpendicular to the chord.

Given: C is the midpoint of the chord AB of the circle with centre of circle at O
To bear witness:OC⊥AB
Construction: Join OA, OB and OC
Proof:
| S.No. | Argument | Reason |
| In ∆OAC and ∆OBC | ||
| 1 | OA = OB | Radii of the same circumvolve |
| 2 | OC = OC | Common side |
| 3 | Air conditioning = BC | Given |
| 4 | ∆OAC ≅ ∆OBC | By SSS congruency |
| 5 | ∠i = ∠2 | Corresponding parts of congruent triangle |
| vi | ∠1 + ∠2 = 180° | Linear pair angles |
| 7 | ∠i = ∠2 = 90° | From statements 5 and half dozen |
| viii | OC ⊥ AB | From statement 7 |
Video Lesson

Solved Examples
Let us see some solved problems on radius and chord of a circle.
Example 1: Detect the radius of the circle if its diameter is sixteen cm.
Solution:
Given,
Bore of circle = 16 cm
Radius of circle = Diameter/2
= 16/2
= 8 cm
Case 2: If the length of the chord of a circle is 8 cm and the perpendicular distance from the center to the chord is iii cm, then what is the radius of the circle?
Solution:
Let us draw a circumvolve every bit per the given information.

Length of the chord = AB = 8 cm
Perpendicular distance = OP = 3 cm
Radius = OA
Nosotros know that, the perpendicular line drawn from the centre of a circle to a chord bisects the chord.
AP = PB = 4 cm
In triangle OPA,
BY Pythagoras theorem,
OA2 = OP2 + APtwo
OA2 = 9 + 16
OA2 = 25
OA = 5
Therefore, radius = 5 cm
To know more about the circle, radius of a circle and eye of the circle download BYJU'S-The Learning App.
Frequently Asked Questions – FAQs
What is the radius of circle?
The length or the altitude from the heart of the circle to anypoint on the circle is called radius. It is denoted by 'r' or 'R'.
What is the relation between radius and bore of a circle?
Radius is equal to half of the diameter of the circle. If the diameter is 10 cm, then radius will be equal to 5 cm.
What is the equation of circumvolve centered at (ane,2) with radius equal 3cm?
Using equation of the circle formula,
(ten-1)ii + (y-ii)2 = 32
(x−one)2 +(y−two)2 = 9
(10ii−2x+1)+(y2−4y+4) = 9
102+ y2−2x−4y−4 = 0
This is the terminal equation.
What is the value of radius, if the area of circumvolve is 78.54 sq cm?
Since, radius = √(Area/π)
Given, area = 78.54 sq.cm and π = 22/7
Therefore,
Radius = √(78.54/(22/7))
Radius = 5 cm (Approximately)
If the circumference of a circle is 100 cms, then find the radius?
Radius = Circumference/2π
R = 100/2π
R = xv.92 cm.
brashearhessium2000.blogspot.com
Source: https://byjus.com/maths/radius-of-a-circle/
Post a Comment for "Draw Circles as Per the Given Number"